ENCONTRAR DUPLICADOS EN UNA LISTA DE DATOS

De las diversas técnicas para hallar los valores duplicados en una lista de datos, estas son las más usadas:

1) Mediante formato condicional, aplicado al rango de datos: Puede establecerse una regla de Formato condicional (menú Formato > Formato condicional…) que mediante una fórmula haga el recuento de ocurrencias de un valor dentro de un rango, y cuándo ese recuento sea mayor que 1 (es decir, se repite), el fondo de la celda se rellene con cierto color, identificando así todos los duplicados.

En este caso selecciona primero el rango B3:B14, elige Formato condicional, completa la fórmula CONTAR.SI(rango,criterio) para la celda B3 y establece la condición >1, define a continuación un formato a aplicar cuando se cumpla esa condición y pulsa Aceptar.

Nota: El rango será aquel que quieras evaluar (en mi caso solo unas pocas celdas), y el criterio la celda para la que buscamos duplicados. Observa que el rango se establece como referencia absoluta (tiene doble $) pero el criterio no; esto es así para que el formato condicional se aplique correctamente a todas las celdas del rango seleccionado inicialmente.

Nota 2: Más abajo encontrarás opciones avanzadas del formato condicional para encontrar y destacar duplicados.

2) Con una columna auxiliar que cuente las ocurrencias de cada valor, mediante la función CONTAR.SI o la función matricial CONTAR. Cuando el valor en la columna auxiliar sea >1 es que se trata de un valor repetido, e indica cuántas veces.

3) Indicar qué filas contienen un valor repetido, en vez del número de repeticiones:

4) Indicar qué filas contienen un valor repetido, pero sin mostrar la primera ocurrencia: Es una variante del anterior, que solo marca como “repetición” a partir de la segunda ocurrencia, para que puedas borrar con seguridad solo las repeticiones. Observa la variación en el rango de la función CONTAR.SI respecto al caso anterior:

5) Identificar si hay valores de la lista A incluidos en la lista B: Si necesitas comparar dos listas separadas de datos para identificar repeticiones de los valores de una en la otra, puedes usar esta fórmula:

6) Otras formas de encontrar duplicados: Si el orden de la lista no es importante, la forma más sencilla de identificar duplicados es primero ordenarla (por ejemplo de menor a mayor si son números, y alfabética si son palabras), y luego poner una sencilla fórmula SI que muestre los duplicados por comparación con la celda inmediatamente superior:

7) Formato condicional avanzado: Estas fórmulas las he tomado de Chip Pearson, como casos especiales de formato condicional relativos a la búsqueda de duplicados:

7.a) Puedes definir la fórmula del formato condicional del punto 1 para destacar los valores que ocurren solamente una vez, en vez de los duplicados.

7.b) Si quieres destacar únicamente la primera ocurrencia de los valores duplicados:

7.c) Si quieres destacar únicamente los duplicados a partir de la segunda ocurrencia:

8) Encontrar el número de valores distintos (no duplicados) de una lista: De nuevo uso una fórmula de Chip Pearson, genial como siempre.

MENUS DESPLEGABLES DE COLOR Y BORDES EN EXCEL

Si sueles trabajar con Bordes y Colores de relleno y de fuente, seguro que usas el desplegable de la barra de formatos para acceder a tus opciones preferidas o más habituales.

Si lo tienes que hacer muy a menudo no resulta eficiente, pero si pinchas en esa pequeña línea de puntos del desplegable y lo arrastras dentro de tu hoja, puedes convertirlo en un menú flotante para facilitar el acceso.

El truco funciona con los desplegables de Bordes, Color de relleno y Color de fuente. Cuando ya no los vayas a seguir usando ciérralos pulsando la X.

BOTON PARA QUITAR LA CUADRICULA DE HOJAS DE CALCULO

Si sueles eliminar la cuadrícula (líneas de división) de tus hojas de cálculo, seguramente usas el método largo: menú Herramientas > Opciones, pestaña Ver, opción Líneas de división:

Sin embargo existe una técnica para añadir un botón a la barra de herramientas que facilite esta tarea.

Simplemente elige el menú Ver  > Barras de Herramientas y selecciona la barra de herramientas de Formularios. Te aparecerá la barra de botones correspondiente, donde uno de ellos sirve exactamente para activar/desactivar las líneas de división de la hoja de cálculo activa.

 

Pulsa Ctrl+Alt, pincha en ese botón, y sin soltar arrástralo sobre tu barra de herramientas habitual (la de Formato por ejemplo). Ya tienes el botón disponible para activar/desactivar la cuadrícula fácilmente.

Extreme #4 - FORMULAS MATRICIALES EN EXCEL

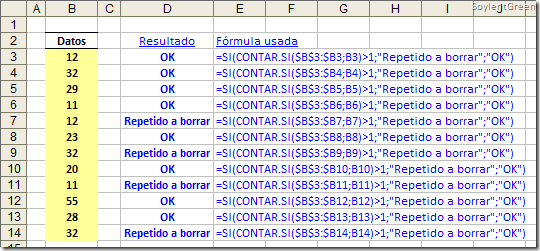
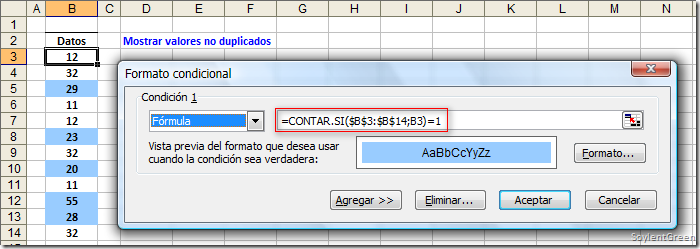
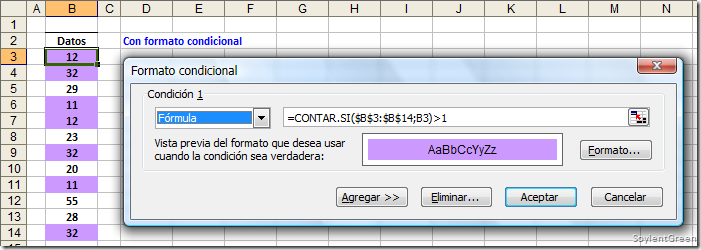
Una fórmula matricial (array formula) realiza varios cálculos en uno o más conjuntos de valores, y devuelve uno o varios resultados. No es mucha la información que puedes encontrar en la Ayuda de Excel sobre esta poderosa herramienta, poco conocida y poco usada.

Una matriz de datos puede ser unidimensional (horizontal o vertical), o tener varias dimensiones:

Si tienes una matriz de cantidades y otra de precios, puedes obtener el total de ingresos por el método básico (multiplicar precios por cantidades y sumarlo), por el método avanzado (usando la función SUMAPRODUCTO, que también trabaja con matrices) o por el método experto (usando una fórmula matricial). Observa la notación de la fórmula matricial {=SUMA(C4:D7*F4:G7)}. Podrían usarse paréntesis para que quede un poco más claro, como {=SUMA((C4:D7)*(F4:G7))}:

La notación de una fórmula matricial puede expresarse como FORMULA (MATRIZ1 (operador) MATRIZ2), su destino puede ser una celda o un conjunto de ellas, y se introduce pulsando Ctrl+May+Enter.

• Fórmula puede ser alguna de las muchas funciones de Excel: SUMA, PROMEDIO, etc
• El operador es la operación que quieres realizar. Para establecer condiciones se utilizan los operadores AND y OR (es decir Y y O), expresados respectivamente con el producto (*) o la suma (+).
• El destino de la fórmula matricial puede ser una sola celda que ofrezca un único resultado, o un conjunto de celdas, que ofrezca una matriz de resultados.

Por ejemplo, una empresa tiene su matriz de cantidades vendidas (C4:D7), su matriz de costes (F4:G7) y su matriz de márgenes porcentuales (I4:J7):

Quiere hacer dos ejercicios: por un lado A) generar su matriz de precios por producto (añadiendo el margen a sus costes), y por otro B) obtener los valores totales de ingresos, gastos y beneficios.

A) Matriz de precios. En este caso queremos obtener como resultado no una celda sino un conjunto de valores. Para ello, seleccionamos las celdas objetivo (L4:M7), escribimos la fórmula que añade los márgenes a la matriz de costes {(F4:G7)*(1+(I4:J7))}, y pulsamos Ctrl+May+Enter. Veremos que las ocho celdas del rango elegido se han resuelto con esa única fórmula:

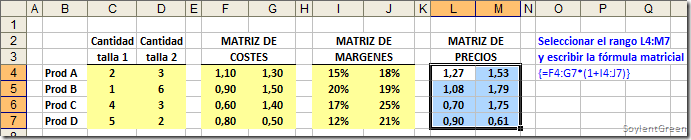
Observa la fórmula usada para añadir los márgenes en porcentaje a los costes, puede resumirse como COSTE x (1+MARGEN %), pero su potencia es que admite matrices de valores como argumentos.

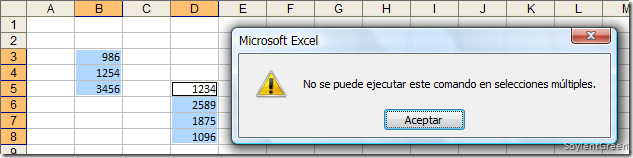
Si intentaras modificar una sola celda del rango resultante, por ejemplo la celda M5, Excel no te dejará porque solo te permitirá modificar el rango (matriz) completo, no una parte de él. Sirve como protección de tus fórmulas matriciales, ya que tienes que modificar todo o nada:

B) Valores de ingresos, costes y resultados: En esta segunda parte, queremos que el resultado aparezca en celdas individuales, no en matrices. Para ello introducimos tres fórmulas matriciales en las celdas G10 (costes), M10 (ingresos) y M12 (beneficio):

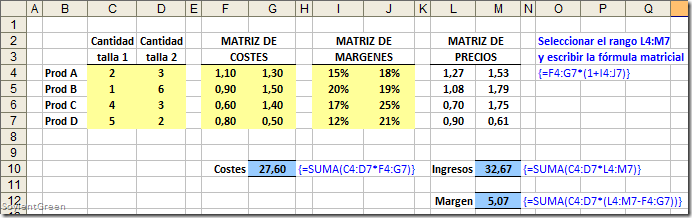
Es cierto, es una forma complicada de hacer algo que podría hacerse más fácil. Pero solo es el principio.

Vamos a otro ejemplo, dadas dos series de datos, por ejemplo los precios por artículo, y el número de artículos que hemos comprado. Queremos obtener el precio medio de los 56 artículos comprados. Generalmente multiplicaremos las dos columnas (cantidad x precio), sumaremos el resultado y lo dividiremos entre el número de artículos (método 1). Alternativamente, conocemos la función SUMAPRODUCTO y la aplicamos a nuestros datos (método 2). Pero también podemos usar las capacidades de Excel de trabajar con matrices de datos, mediante funciones matriciales (método 3):

Para la fórmula matricial las funciones y sus argumentos son las normales en Excel, pero recordando que trabajamos con matrices de datos. Además como he dicho antes debemos indicar claramente que se trata de una operación con matrices; para eso, en vez de pulsar Enter cuando hemos acabado de escribirla, usaremos Control+Mayúsculas+Enter. Eso añadirá llaves de apertura y cierre { } a nuestra expresión, lo cual sirve para avisar que se trata de una fórmula matricial.

Nota: Incluso cuando edites de nuevo tu fórmula matricial en la barra de fórmulas, tendrás que validarla pulsando Ctrl+May+Enter o dará error. Recuerda que las llaves de apertura y cierre no hay que escribirlas.

Sigues pensando: “Vaya cosa, una forma complicada de hacer algo que puedo hacer más fácil con lo que ya sabía”. Tienes razón, los problemas de trabajar con fórmulas matriciales no compensan su aparente utilidad en este ejemplo. Pero era solo otro ejemplo sencillo, vamos a ver ahora la potencia de esta herramienta.

1) USO PARA DISCRIMINAR ERRORES EN SERIES DE DATOS:

Tengo una serie de 7 datos, pero uno muestra error en la hoja de cálculo. Sabemos que no puede calcularse el promedio de una serie si alguno da error, pero puedo usar la fórmula matricial para obtener el promedio de los datos:

Vemos que el PROMEDIO normal no ofrece ningún resultado, mientras que usando la fórmula matricial no importa que haya elementos en error. Lo que la función condicional SI(ESERROR()) de la fórmula matricial indica es que si algún elemento de la matriz da error, debe tomarse el 0 (cero) como valor en el primer caso [promedio de siete elementos 13, 18, 25, 17, 0, 15, 16], y como elemento vacío (no computable) en el segundo [promedio de seis elementos 13, 18, 25, 17, 15, 16]. No se me ocurre una forma más fácil de evitar celdas en error, así que después de todo parece que las matriciales tienen alguna utilidad ¿eh?. Lo mismo sirve para otras funciones habituales con las que obtendrías errores:

2) APLICACION A RANGOS DE DATOS, USANDO CONDICIONES:

Una empresa paga un bonus a sus agentes, del 10% si sus márgenes superan la media de la empresa, y del 5% si están por debajo de la media. Esto puede calcularse de la forma tradicional, sin complicaciones, pero también con fórmulas matriciales:

• Se han definido tres rangos (VENTAS, MARGEN, MGMEDIO). Los dos primeros se usarán como matrices de datos, y el tercero como valor de comparación.
• Para hacer que una fórmula matricial se aplique no a una solo celda, sino a una matriz de resultados (en este caso será el rango G3:G10, cada uno de los agentes), lo primero que hay que hacer es seleccionar la matriz de salida (G3:G10) y escribir la fórmula matricial en la primera celda del rango (G3). La fórmula elegida es una condición {=SI(MARGEN/VENTAS>MGMEDIO;MARGEN*10%;MARGEN*5%)} tal que para cada elemento de la matriz evalúe si el margen del agente es superior o inferior a la media, y en cada caso aplique el 10% o el 5% de bonus. Pulsamos Ctrl+May+Enter y el resto de celdas seleccionadas (G4 a G10) se rellenará con la misma fórmula matricial.

 

En este caso también es más fácil el método tradicional, y escribir una condición simple SI en la columna G para aplicar el porcentaje de bonus, pero solo quiero mostrar otra forma de hacerlo.

3) OTROS EJEMPLOS:

¿Aún no le ves la utilidad?. Supongamos que tienes una lista de miles de frases, y quieres saber cuál es la longitud en caracteres de la frase más larga. Habitualmente añadirías una columna a la derecha de esa lista de palabras, aplicarías la función =LARGO(celda) a cada una de las frases, y luego buscarías el mayor valor de esta nueva columna. Pues con una función matricial te bastaría con {=MAX(LARGO(rango)} para obtener el mismo resultado.

Vamos a otro ejemplo. Dicen que las fórmulas matriciales deben emplearse sobre todo para evaluar (contar y sumar) celdas basándose en criterios múltiples. Una empresa vende tres productos y tiene tres vendedores. Cada día revisan el listado de ventas del día anterior, y quieren hacer una tabla resumen de unidades vendidas por producto y vendedor:

• Opción 1: hacen una tabla dinámica y se olvidan de preocupaciones.
• Opción 2: son maestros de Excel, han leído este post y deciden aplicar fórmulas matriciales.

En este caso usaremos tres rangos de datos (PROD, VEND, UDS) y una única celda como matriz de salida (Q16). Luego llenaremos hacia abajo y hacia la derecha para completar la tabla.

Nota: La fórmula SUMA((PROD=P16)*(VEND=Q15)*(UDS)) ofrecerá la suma de unidades que cumplen las condiciones de Producto y Vendedor establecidas.

El siguiente ejemplo lo he tomado libremente de da TAB.IS.ON, una web muy buena sobre Excel. Primero se obtienen mediante fórmulas matriciales los valores máximos y mínimos de ventas de acuerdo a ciertos criterios (por producto y región). Y luego se riza el rizo al obtener el Producto y la Región correspondientes a los valores de ventas máximas y mínimas respectivamente. La fórmula usada es fantástica:

• Observa el uso de matrices en la función SUMAR.SI de las celdas F3 y F9, en modo que sus tres argumentos, tanto el rango de comparación, como el criterio, así como el rango de suma, son matrices.
• Las fórmulas más largas son geniales. Lo que hace primero es comprobar SI la SUMA de ventas de un determinado Producto es igual al valor máximo que puede tener; si el resultado es cierto, devuelve el número de su fila. Usando la función MAX se halla la FILA donde el nombre del Producto aparece por última vez, y luego la función DESREF nos dará el nombre del Producto correspondiente a esa fila.

4) OTRAS OPERACIONES UTILES CON FORMULAS MATRICIALES:

4.1) Suma de resultados otras funciones Excel aplicadas sobre matrices: Por ejemplo sumas de rangos redondeados, de valores absolutos, etc.

 

 

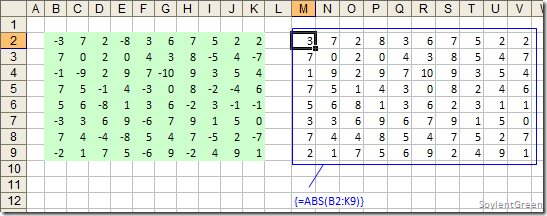
4.3) Convertir todo una matriz de números en una nueva matriz de valores absolutos: Para ello elegimos como rango de salida una matriz del mismo tamaño que el rango origen, y escribimos la fórmula matricial {ABS(rango)}. Es un método mucho más rápido que aplicar condiciones.

4.4) Sumas o Recuentos basados en múltiples condiciones: Observa la última fórmula, y cómo obtiene el recuento final (también la he tomado de da TAB.IS.ON).

4.5) Transformaciones complejas de matrices de datos, basadas en múltiples condiciones:

Puedes anidar sucesivas condiciones SI para tratar cada valor de la matriz origen según reglas especiales. Recuerda que el asterisco (*) equivale al operador AND, es decir, exige que se cumplan ambas condiciones. Puedes asimismo usar el operador OR, con la suma (+).

4.6) Contar ocurrencias de una cadena de texto en listas de palabras, evaluar características:

4.7) Sumar una cadena de números a los que se ha dado formato de texto: Todos nos hemos encontrado con números que venían formateados como texto, y para los que las funciones normales no funcionarán hasta no transformar en números reales esos “falsos números”. Pues bien, con una fórmula matricial usando la función VALUE, puedes hacer estas operaciones sin ninguna otra transformación.

Esto no acaba aquí, seguiré poniendo ejemplos de esta poderosa herramienta de fórmulas matriciales.

HIPERVINCULOS EN UNA HOJA DE CALCULO

Se pueden crear en Excel vínculos a otras hojas del mismo libro. De esa forma, si tu libro tiene muchas hojas, puedes incluir un “acceso directo” en una hoja para poder desplazarte rápidamente a otra.

Para hacerlo, selecciona el menú Insertar > Hipervínculo. Tienes que indicar:

1. Que quieres enlazar a algún lugar del documento activo (tu libro abierto).
2. Elige la hoja de cálculo de destino de tu hipervínculo (=destino general).
3. Elige la celda de esa hoja de cálculo que quieres activar (=destino específico).
4. Dale un nombre al enlace para recordar qué es lo que hace (por ejemplo el destino).

El hipervínculo aparece en azul y subrayado, y el cursor se modifica cuando pasas sobre él:

Nota: Recuerda que si cambias el nombre de la hoja de destino, el hipervínculo quedará roto.

Nota: Puedes modificar el formato del hipervínculo. Como la celda con hipervínculo no puede seleccionarse con el cursor, tienes que situarte debajo y pulsar Cursor Arriba (o bien usando el ratón pero presionando la tecla Ctrl para que no se active el hipervínculo). Entonces puedes aplicar el formato que desees.

Nota: Las celdas con hipervínculos pueden copiarse y moverse, y el enlace se copia y mueve con ellas.

COPIAR VARIOS RANGOS A LA VEZ

Si intentas copiar dos rangos separados del celdas de una misma hoja (por ejemplo B3:B5 y D5:D8 en mi hoja), verás que Excel da un error porque esa funcionalidad no es posible.

Sin embargo tiene algunas excepciones que pueden utilizarse para casos concretos. Estas excepciones están relacionadas con que los rangos se encuentren todos en las mismas filas y/o columnas.

Así, es posible copiar dos rangos separados de celdas si se encuentran en una misma columna, con la peculiaridad de que Excel elimina las filas en blanco (bastante útil para evitarte tener que borrar líneas en blanco de una larga lista de números en columna):

De la misma forma, puedes copiar varios rangos pertenecientes a distintas columnas, con tal de que estos se encuentren en las mismas filas. Excel los agrupa eliminando las columnas vacías:

TITULO VARIABLE DE GRAFICO

Puedes hacer que el título de tu gráfico Excel esté ligado al contenido de una celda concreta de la hoja de cálculo, para poder cambiarlo fácilmente.

Selecciona el título del gráfico, ve a la barra de fórmulas y escribe el signo = (igual). Pincha ahora en la celda que contenga lo que quieras que sea el título del gráfico (en mi caso la B2) y pulsa Enter.

Listo, cada vez que modifiques la celda B2 el título del gráfico cambiará.

Nota: Verás que no sirve escribir a mano =B2 en la barra de fórmulas, tienes que seleccionar la celda con el ratón (o escribir la referencia a la celda incluyendo el nombre de la hoja seguida del signo de exclamación !).